
TSM Resources
ATM: MT-274
"Autograph - a new resource for all seasons"
An all-device web version is due in the New Year. Meanwhile Autograph 5 will run all these files,
and it can be downloaded for free on www.completemaths.com, running on all Windows computers and pre-Catalina IOS
Any device will run all these videos.
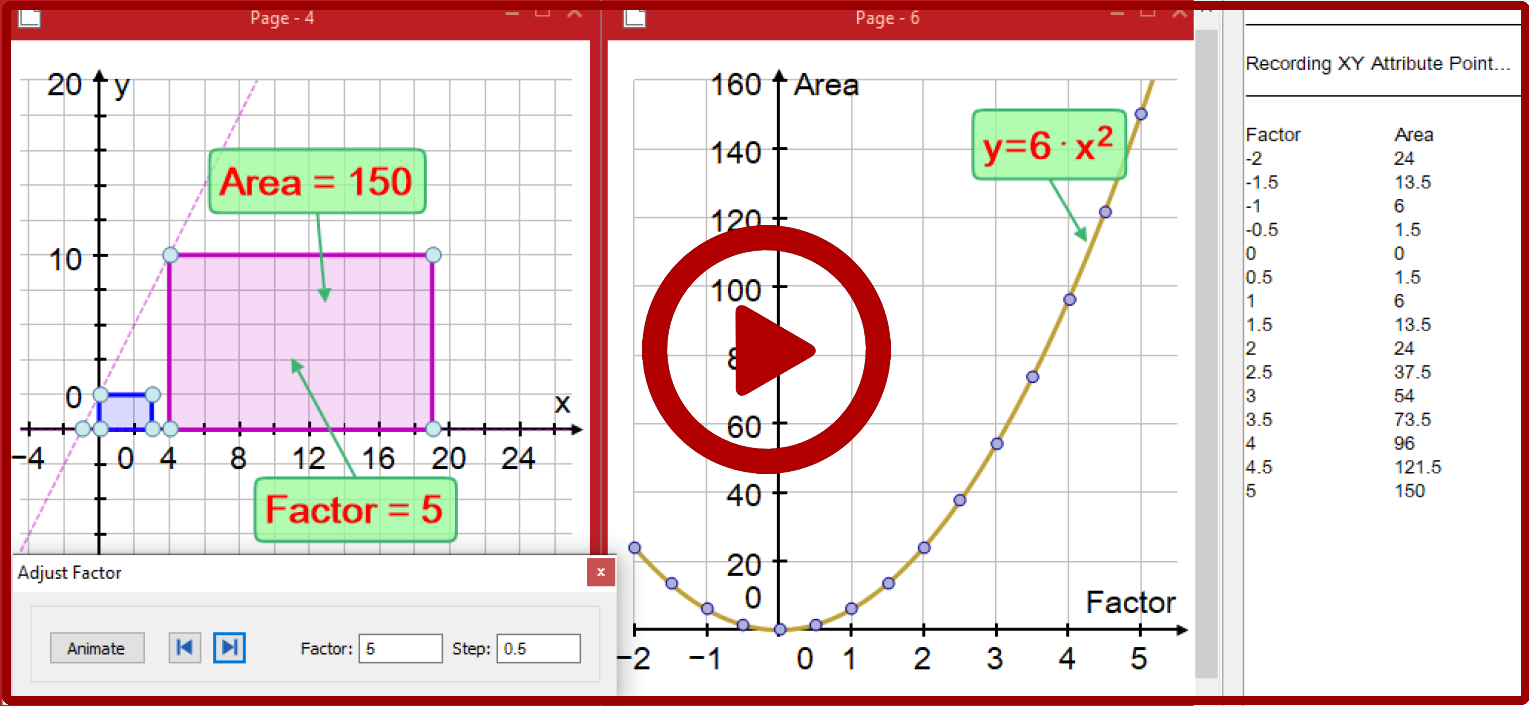
1. A new feature of Autograph is the ability to define a new ‘XY’ point using attributes of other objects.
Here its coordinates are: the enlargement factor, ‘k’ and the enlarged area.
As ‘k’ is animated the values can be recorded and plotted to confirm a quadratic relationship (the host shape has area 6).
Autograph files:
Enlargement
Recording
2. Single variable: points can be dropped in and moved about to help understand the box plot and its outliers.
Autograph file:
raw-data

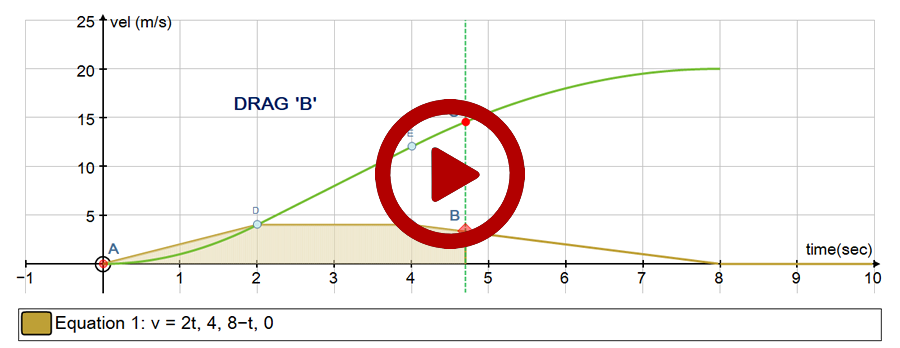
3. Velocity-Time graph entered as a piece-wise function. The distance travelled is generated from the area to time ‘t’
Autograph file:
velocity-time
4. Just 6 points added which can be moved about to help understand the mean, best fit line and correlation.
Autograph file;
scatter diagram

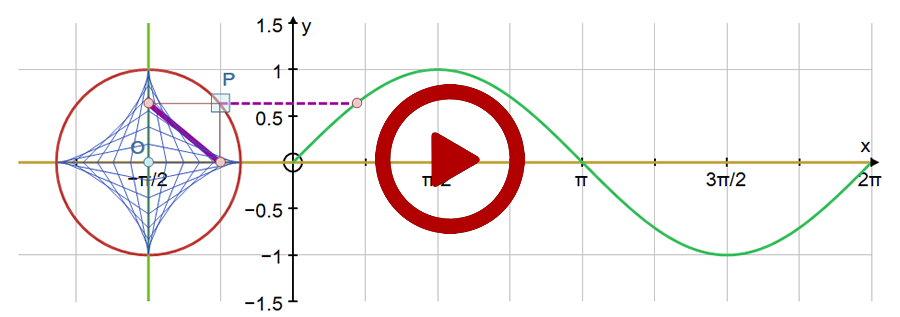
5. The very visible link between the sine graph and the unit circle, together with a locus of a chord of length 1.
Autograph files:
unit circle
circle locus
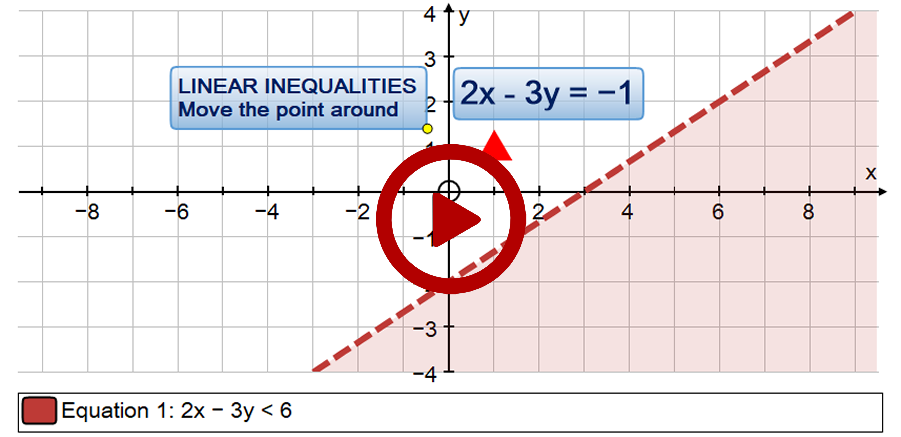
6. Exploring an inequality: using the calculator to evaluate 2x–3y for a moveable point: more than 6 on the right!
Autograph file:
inequality
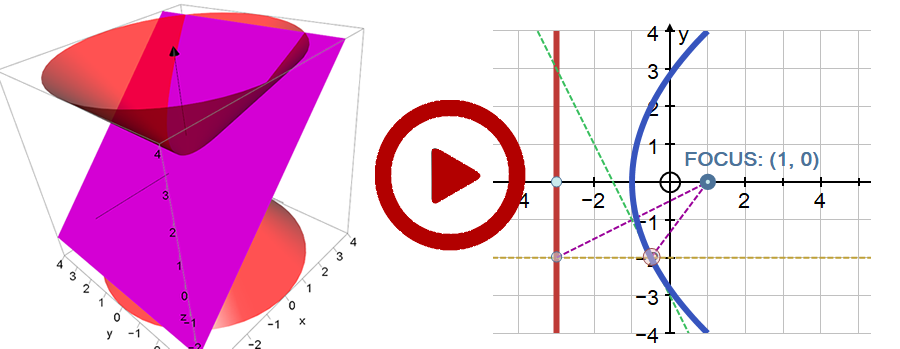
7. A cone and a plane illustrating the conic sections, together with the construction of a parabola.
Autograph files:
conics-3D
conics-eqns
conics-polar
parabola
8. I have always wanted a 3D Argand Diagram and here it is!
Three views of the roots of
x² – 2x + c = 0
when ‘c’ = 2:
(a) in the x-y plane ‘no solutions!’,
(b) in the 2D Argand diagram with ‘z’ entered as
1 ± √(1 – c)

